Hoekverplaatsingsformules en opgeloste oefeningen
de hoekverplaatsing het wordt gegenereerd wanneer een object beweegt volgens een pad of pad dat de vorm van een cirkel heeft. Het is anders dan de verplaatsing; terwijl de hoekverplaatsing de afgelegde hoek meet, meet de verplaatsing de afstand.
Voor het berekenen van de hoekverplaatsing van een object dat langs een omtrek beweegt, kunnen twee manieren worden gebruikt: als de begin- en eindhoek bekend is, dan is de hoekverplaatsing de aftrekking tussen de uiteindelijke hoek en de beginhoek..
Als de lengte van de verplaatsing (lengte van de omtrekboog afgelegd) en de straal van de omtrek bekend zijn, wordt de hoekverplaatsing gegeven door θ = l / r.
index
- 1 Formules
- 2 oefeningen
- 2.1 Eerste oefening
- 2.2 Tweede oefening
- 2.3 Derde oefening
- 3 referenties
formules
Om de hierboven beschreven formules te verkrijgen, ziet u de volgende afbeeldingen:
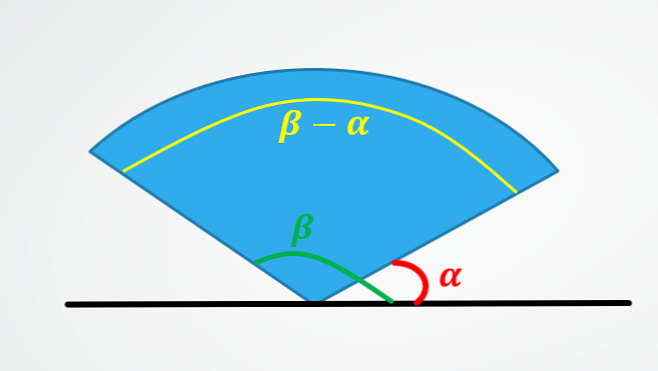
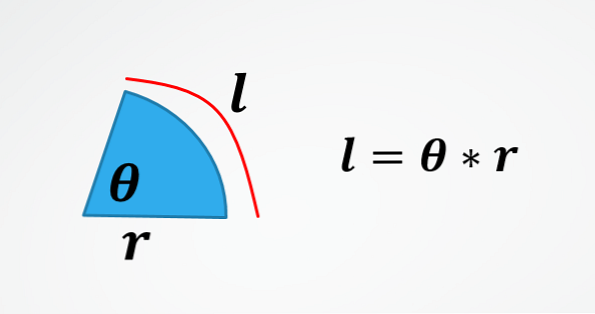
De eerste toont waarom de hoekverplaatsing gelijk is aan het aftrekken van de uiteindelijke hoek minus de beginhoek.
In de tweede afbeelding staat de formule voor de lengte van een cirkelboog. Daarom krijgt u door het wissen van θ de formule die aan het begin is beschreven.
opleiding
Hieronder staan enkele oefeningen waarbij de definitie van hoekverplaatsing moet worden toegepast en waarbij de hierboven beschreven formules worden gebruikt.
Eerste oefening
Juan heeft een afstand van 35 meter afgelegd op een cirkelvormig looppad waarvan de straal gelijk is aan 7 meter. Bereken de hoekverplaatsing die Juan heeft gemaakt.
oplossing
Omdat de afstand van de afgelegde boog en de straal van de omtrek bekend zijn, kan de tweede formule worden toegepast om de hoekverplaatsing van Juan te kennen. Met behulp van de hierboven beschreven formule heb je dat θ = 35/7 = 5 radialen.
Tweede oefening
Als je hebt dat Mario in zijn voertuig de halve cirkelbaan heeft afgelegd, wat is dan de hoekverplaatsing die Mario heeft gedaan??
oplossing
In deze oefening wordt de eerste formule toegepast. Omdat bekend is dat Mario de helft van de baan heeft afgelegd, kan worden aangenomen dat hij de race in de 0 ° -hoek begon en toen hij het midden van de cirkel bereikte, heeft hij 180 ° afgelegd. Daarom is het antwoord 180 ° -0 ° = 180 ° = π radialen.
Derde oefening
María heeft een rond zwembad. Je hond loopt rond het zwembad over een afstand van 18 meter. Als de straal van het zwembad 3 meter is, wat is dan de hoekverdraaiing van Maria's mascotte??
oplossing
Omdat het zwembad cirkelvormig is en u de straal ervan kent, kunt u doorgaan met het gebruik van de tweede formule.
Het is bekend dat de straal gelijk is aan 3 meter, en de afgelegde afstand door het huisdier is gelijk aan 18 meter. Daarom is de uitgevoerde hoekverplaatsing gelijk aan θ = 18/3 = 6 radialen.
referenties
- Basto, J. R. (2014). Wiskunde 3: Elementaire analytische meetkunde. Patria Editorial Group.
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Wiskunde: een probleemoplossende aanpak voor leraren in het basisonderwijs. López Mateos-bewerkers.
- Bult, B., & Hobbs, D. (2001). Wiskunde lexicon (geïllustreerd ed.). (F.P. Cadena, Trad.) Edities AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometrie. Hervorming van de bovenste cyclus van de E.G.B. Ministerie van Onderwijs.
- Schneider, W., & Sappert, D. (1990). Praktische technische tekeninghandleiding: inleiding tot de basis van industriële technische tekening. Reverte.
- Thomas, G. B., & Weir, M.D. (2006). Berekening: verschillende variabelen. Pearson Education.


