Hoeveel randen heeft een zeshoekig prisma?
Weten hoeveel randen heeft een hexagonaal prisma de betekenis van "rand", "prisma" en "zeshoekig" moet bekend zijn. De eerste twee concepten zijn algemene definities, en het derde concept heeft te maken met de vorm van de geometrische figuur.
Bij het spreken over zeshoekig wordt een zeshoek (veelhoek) genoemd. Het voorvoegsel "hexa" geeft aan dat de polygoon zes zijden heeft.

Een rand is een rand van een object. Geometrisch is het een lijn die twee opeenvolgende hoekpunten van een meetkundige figuur met elkaar verbindt.
Een prisma is een geometrisch figuur begrensd door twee bases die evenwijdige en gelijke polygonen zijn en hun zijvlakken parallellogrammen.
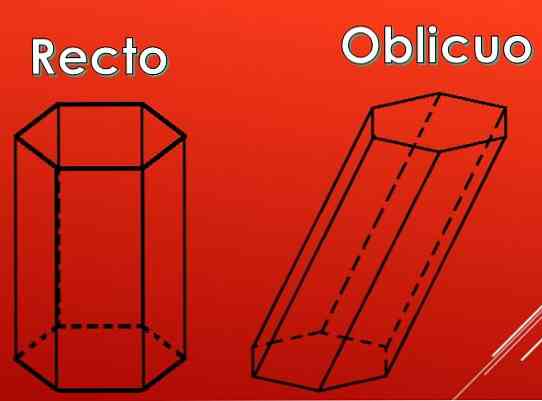
In de volgende afbeelding kan worden gezien dat de zijvlakken van een hexagonaal prisma rechthoeken kunnen zijn, maar ze kunnen ook parallellogrammen zijn.
Afhankelijk van het type parallellogram kunnen de premies worden ingedeeld in twee soorten: recht en schuin.
Hoe de randen van een zeshoekig prisma te tellen?
Het aantal randen dat een hexagonaal prisma zal hebben, zal niet veranderen als het een recht of schuin prisma is. Ook hangt het aantal randen niet af van de lengte van de zijkanten.
Het tellen van de randen van een zeshoekig prisma kan op verschillende manieren worden gedaan. Hier zijn twee manieren:
1- Ontleed het prisma
Een manier om de randen te tellen is door het hexagonale prisma in zijn twee bases en zijn zijvlakken te ontbinden. Op deze manier krijg je twee zeshoeken en een parallellogram met vijf binnenlijnen.
Elke zeshoek heeft zes randen, daarom heeft het prisma meer dan 12 randen.
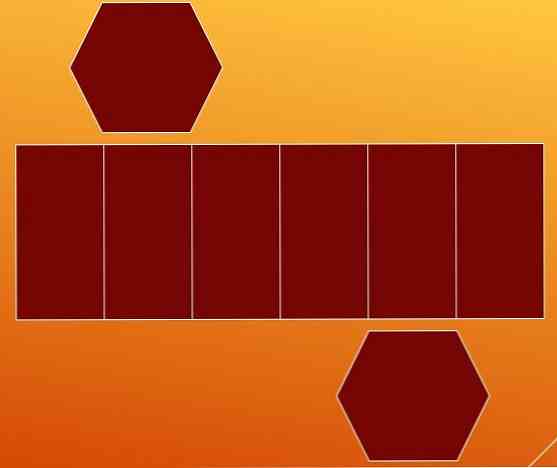
Op het eerste gezicht wordt gedacht dat het parallellogram negen randen bevat (zeven verticale en twee horizontale). Maar het is handig om te stoppen om deze zaak te analyseren.
Wanneer het parallellogram wordt gebogen om het prisma te vormen, kan worden gezien dat de eerste lijn aan de linkerkant zal samenkomen met de laatste regel aan de rechterkant, waarmee beide lijnen een enkele rand vertegenwoordigen.
Maar hoe zit het met de twee horizontale lijnen?
Als alle stukjes opnieuw zijn samengevoegd, worden de horizontale lijnen samengevoegd, elk met de zes randen van elke zeshoek. Om deze reden zou het fout zijn om ze apart te tellen.
Het parallellogram bevat dus zes randen van het prisma die, samen met de 12 randen die aan het begin worden geteld, in totaal 18 randen geeft.
2.- Elke rand projecteren
Een andere manier, veel eenvoudiger om de randen te tellen, is het feit dat de basis van de zeshoekige prisma's zeshoeken zijn, dan heeft elke basis zes randen.
Aan de andere kant, vanaf elke top van een zeshoek, wordt een enkele rand geprojecteerd op de overeenkomstige top van de andere zeshoek; dat wil zeggen, er zijn zes randen die de ene basis met de andere verbinden.
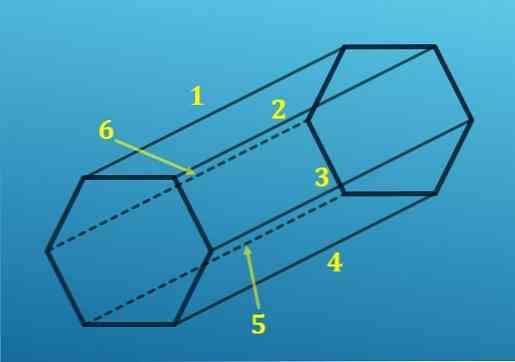
Door alle randen toe te voegen, krijgt u in totaal 18 randen.
conclusie
Er kan worden aangetoond dat het aantal randen van een prisma gelijk is aan drie keer het aantal randen dat de polygoon die het vormt.
Daarom heeft een vijfhoekig prisma 3 * 5 = 15 randen, een heptagonaal prisma heeft 3 * 7 = 21 randen en kan het dus op elk prisma worden toegepast.
referenties
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Wiskunde: een probleemoplossende aanpak voor leraren in het basisonderwijs. López Mateos-bewerkers.
- Fregoso, R. S., & Carrera, S. A. (2005). Wiskunde 3. Redactie Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Wiskunde 6. Redactie Progreso.
- Gutiérrez, C. T., & Cisneros, M.P. (2005). 3e Wiskunde Cursus. Redactie Progreso.
- Kinsey, L., & Moore, T.E. (2006). Symmetrie, vorm en ruimte: een inleiding tot de wiskunde door middel van geometrie (geïllustreerd, herdrukt). Springer Science & Business Media.
- Mitchell, C. (1999). Dazzling Math Line Designs (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Ik teken 6º. Redactie Progreso.


