Hoeveel assen van Symmetrie heeft een cirkel?
de symmetrie-assen van een cirkel Ze zijn oneindig. Deze assen zijn diegene die elke geometrische vorm in twee exact gelijke helften verdelen.
En een cirkel bestaat uit alle punten waarvan de afstand tot een vast punt kleiner is dan of gelijk is aan een bepaalde waarde "r".
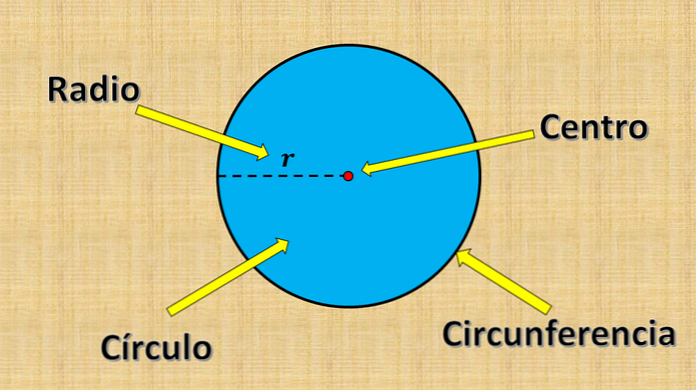
Het hierboven genoemde vaste punt wordt midden genoemd en de waarde "r" wordt straal genoemd. De straal is de grootste afstand die er kan zijn tussen een punt op de cirkel en het midden.
Aan de andere kant wordt elk lijnsegment waarvan de uiteinden aan de rand van de cirkel (omtrek) liggen en door het midden gaan, de diameter genoemd. De meting is altijd gelijk aan tweemaal de straal.
Cirkel en omtrek
Verwar een cirkel niet met een cirkel. De omtrek verwijst alleen naar de punten op afstand "r" van het centrum; dat is, alleen de rand van de cirkel.
Bij het zoeken naar de assen van symmetrie is het echter onverschillig of je met een cirkel of met een cirkel werkt.
Wat is een symmetrie-as?
Een symmetrie-as is een lijn die in twee gelijke delen een bepaalde geometrische figuur verdeelt. Met andere woorden, een symmetrieas gedraagt zich als een spiegel.
Schachten van symmetrie van een cirkel
Als je een cirkel waarneemt, ongeacht de straal, kun je zien dat niet elke lijn die er doorheen gaat een symmetrieas is.
Geen van de lijnen in de volgende afbeelding is bijvoorbeeld een symmetrieas.
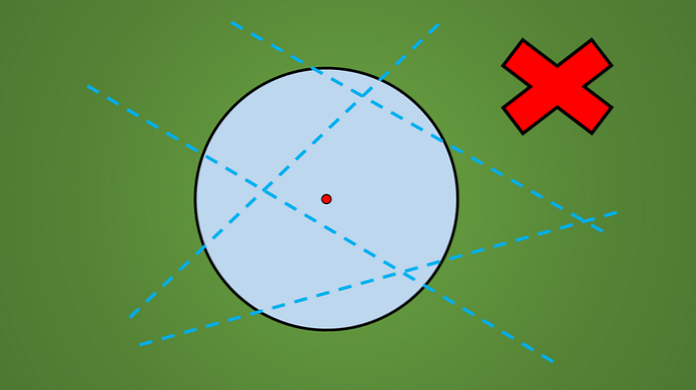
Een eenvoudige manier om te controleren of een lijn een symmetrieas is of niet, is door de geometrische figuur loodrecht op de tegenovergestelde kant van de lijn te reflecteren.
Als de reflectie niet past bij de oorspronkelijke figuur, is die lijn geen symmetrieas. De volgende afbeelding illustreert deze techniek.
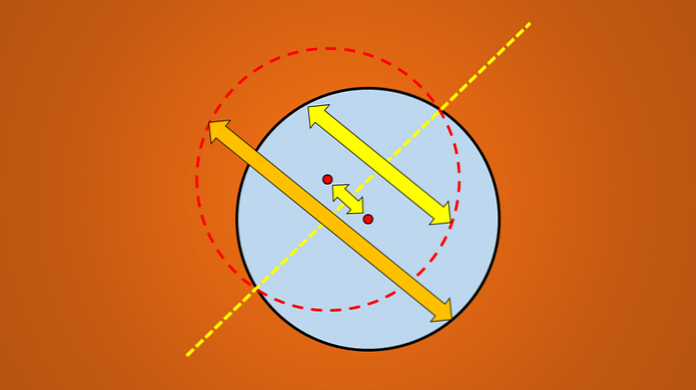
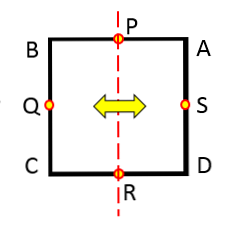
Maar als het volgende beeld wordt beschouwd, is het algemeen bekend dat de getekende lijn een symmetrieas van de cirkel is.
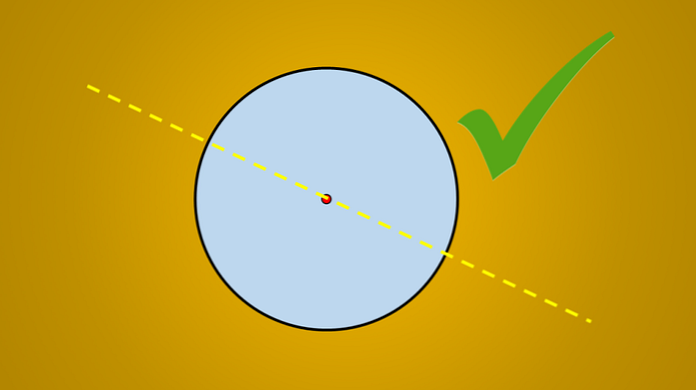
De vraag is: zijn er meer assen van symmetrie? Het antwoord is ja. Als u deze lijn 45 ° tegen de klok in draait, is de verkregen lijn ook een symmetrieas van de cirkel.
Hetzelfde gebeurt als u 90 °, 30 °, 8 ° en in het algemeen een willekeurig aantal graden draait.
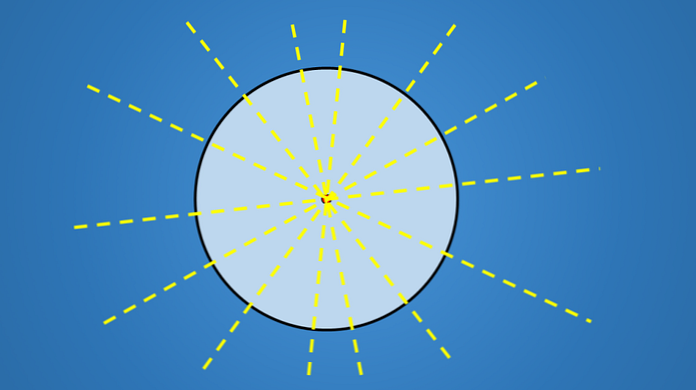
Het belangrijkste aan deze lijnen is niet de neiging die ze hebben, maar ze gaan allemaal door het midden van de cirkel. Daarom is elke lijn met een diameter van de cirkel een symmetrieas.
Omdat een cirkel een oneindig aantal diameters heeft, heeft deze dus een oneindig aantal assen van symmetrie.
Andere geometrische figuren, zoals een driehoek, een vierhoek, een vijfhoek, een zeshoek of een andere veelhoek, hebben een eindig aantal assen van symmetrie.
De reden waarom een cirkel een oneindig aantal assen van symmetrie heeft, is dat deze geen zijden heeft.
referenties
- Basto, J. R. (2014). Wiskunde 3: Elementaire analytische meetkunde. Patria Editorial Group.
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Wiskunde: een probleemoplossende aanpak voor leraren in het basisonderwijs. López Mateos-bewerkers.
- Bult, B., & Hobbs, D. (2001). Wiskunde lexicon (geïllustreerd ed.). (F.P. Cadena, Trad.) Edities AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometrie. Hervorming van de bovenste cyclus van de E.G.B. Ministerie van Onderwijs.
- Schneider, W., & Sappert, D. (1990). Praktische technische tekeninghandleiding: inleiding tot de basis van industriële technische tekening. Reverte.
- Thomas, G. B., & Weir, M.D. (2006). Berekening: verschillende variabelen. Pearson Education.


