Capillariteitskarakteristieken en voorbeeld in het water

de capillariteit Het is een eigenschap van vloeistoffen die het mogelijk maakt om door buisvormige gaten of poreuze oppervlakken te bewegen, zelfs tegen de zwaartekracht in. Hiervoor moet er een evenwicht en coördinatie zijn tussen twee krachten die verband houden met de vloeibare moleculen: cohesie en adhesie; met deze twee een fysieke reflectie genaamd oppervlaktespanning.

De vloeistof moet in staat zijn om de inwendige wanden van de buis of de poriën van het materiaal waardoorheen het beweegt te bevochtigen. Dit gebeurt wanneer de adhesiekracht (vloeistofwand van de capillaire buis) groter is dan de intermoleculaire cohesiekracht. Bijgevolg creëren de vloeibare moleculen sterkere interacties met de atomen van het materiaal (glas, papier, enz.) Dan daartussen.

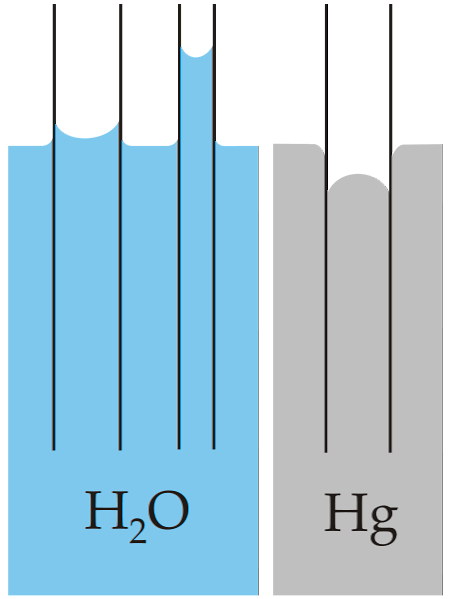
Het klassieke voorbeeld van capillariteit wordt geïllustreerd door de vergelijking van deze eigenschap voor twee zeer verschillende vloeistoffen: water en kwik.

De bovenste afbeelding laat zien dat het water door de wanden van de buis omhoog gaat, wat betekent dat het hogere adhesiekrachten heeft; terwijl het tegenovergestelde gebeurt met kwik, omdat de cohesieve, metallieke hechtingskrachten voorkomen dat het glas wordt bevochtigd.

Om deze reden vormt water een concave meniscus, en kwik een convexe meniscus (koepelvormig). Er moet ook worden opgemerkt dat hoe kleiner de straal van de buis of de sectie waardoor de vloeistof beweegt, hoe groter de hoogte of afgelegde afstand is (vergelijk de hoogtes van de waterkolommen voor beide buizen).

index

• 1 Kenmerken van capillariteit
  • 1.1 - Oppervlak van de vloeistof
  • 1.2 - Hoog
  • 1.3 - Oppervlaktespanning
  • 1.4 -Radio van het capillair of de porie waar de vloeistof opstijgt
  • 1.5 - Contacthoek (θ)
• 2 Capillariteit van water
  • 2.1 Over planten
• 3 referenties

Kenmerken van capillariteit

-Oppervlak van de vloeistof

Het oppervlak van de vloeistof, om te zeggen water, in een capillair is hol; dat wil zeggen, de meniscus is hol. Deze situatie doet zich voor omdat het resultaat van de krachten uitgeoefend op watermoleculen nabij de wand van de buis hier naartoe is gericht.

In alle meniscus is er een contacthoek (θ), de hoek die de wand van de capillaire buis vormt met een lijn die raakt aan het oppervlak van de vloeistof op het contactpunt.

Hechting en cohesiekrachten

Als de adhesiekracht van de vloeistof op de capillaire wand de overhand heeft op de intermoleculaire cohesiekracht, is de hoek θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.

Wanneer een druppel water op het oppervlak van een schoon glas wordt geplaatst, verspreidt zich water over het glas, zodat θ = 0 en cos θ = 1.

Als de intermoleculaire cohesiekracht de overhand heeft op de hechtkracht van de vloeistofwand van het capillair, bijvoorbeeld in kwik, is de meniscus convex en heeft de hoek θ een waarde> 90º; het kwik bevochtigt de capillaire wand niet en daalt daarom door zijn binnenwand.

Wanneer een druppel kwik op het oppervlak van een schoon glas wordt geplaatst, behoudt de druppel zijn vorm en de hoek θ = 140º.

-hoogte

Water stijgt door de capillaire buis tot een hoogte (h), waarin het gewicht van de waterkolom compenseert voor de verticale component van de intermoleculaire cohesiekracht.

Naarmate er meer water stijgt, zal er een punt komen waarop de zwaartekracht de stijging zal stoppen, zelfs met oppervlaktespanning die in uw voordeel werkt.

Wanneer dit gebeurt, kunnen de moleculen niet verder omhoog langs de binnenmuren "klimmen" en worden alle fysieke krachten gelijkgemaakt. Aan de ene kant heb je de krachten die de opkomst van water bevorderen, en aan de andere kant je eigen gewicht dat het naar beneden duwt.

Jurin's Law

Dit kan als volgt wiskundig worden geschreven:

2 π rΥcosθ = ρgπr²h

Waar de linkerkant van de vergelijking afhangt van de oppervlaktespanning, waarvan de grootte ook gerelateerd is aan de cohesie of intermoleculaire krachten; Cosθ vertegenwoordigt de contacthoek en r de straal van het gat waardoor de vloeistof omhoog gaat.

En aan de rechterkant van de vergelijking hebben we de hoogte h, de zwaartekracht g en de dichtheid van de vloeistof; dat zou het water zijn.

Opruimen dan h je hebt

h = (2Υcosθ / ρgr)

Deze formulering staat bekend als de wet van Jurin, die de hoogte definieert die wordt bereikt door de vloeistofkolom in het capillair, wanneer het gewicht van de vloeistofkolom wordt uitgebalanceerd met de kracht van ascensie door capillariteit.

-Oppervlaktespanning

Water is een dipolair molecuul, vanwege de elektronegativiteit van het zuurstofatoom en de moleculaire geometrie. Hierdoor wordt het deel van het watermolecuul waar de zuurstof zich bevindt negatief geladen, terwijl het deel van het watermolecuul, dat de 2 waterstofatomen bevat, positief wordt geladen.

De moleculen in de vloeistof reageren dankzij dit door meerdere waterstofbruggen, waardoor ze bij elkaar blijven. Echter, de watermoleculen die zich in het grensvlak water bevinden: lucht (oppervlak), zijn onderhevig aan een netto aantrekking door de moleculen van de vloeibare sinus, niet gecompenseerd door de zwakke aantrekking met de luchtmoleculen..

Daarom worden de watermoleculen van het grensvlak onderworpen aan een aantrekkingskracht die de neiging heeft watermoleculen uit het grensvlak te verwijderen; dat wil zeggen, de waterstofbruggen gevormd met de moleculen in de bodem slepen die op het oppervlak. Aldus tracht de oppervlaktespanning het oppervlak van het water: luchtgrensvlak te verminderen.

Verbonden met h

Als je naar de vergelijking van de wet van Jurin kijkt, zul je zien dat h recht evenredig is met Υ; daarom, hoe groter de oppervlaktespanning van de vloeistof, hoe groter de hoogte die kan stijgen door een capillair of porie van een materiaal.

Zo kan worden verwacht dat voor twee vloeistoffen, A en B, met verschillende oppervlaktespanningen, degene met de hoogste oppervlaktespanning tot een hogere hoogte stijgt.

Uit dit punt kan worden geconcludeerd dat een hoge oppervlaktespanning de belangrijkste eigenschap is die de capillaire eigenschap van een vloeistof bepaalt.

-Straal van de capillair of porie waar de vloeistof opkomt

De observatie van de Wet van Jurin geeft aan dat de hoogte bereikt door een vloeistof in een capillair of porie omgekeerd evenredig is met de straal van hetzelfde.

Daarom, hoe kleiner de straal, hoe groter de hoogte die de vloeistofkolom door capillaire werking zal bereiken. Dit is direct te zien in de afbeelding waar water wordt vergeleken met kwik.

In een glazen buis met een straal van 0,05 mm radius, zal de waterkolom door capillariteit een hoogte bereiken van 30 cm. In capillaire buizen met een straal van 1 μm met een zuigdruk van 1,5 x 10³ hPa (wat gelijk is aan 1,5 atm) komt overeen met een berekening van de hoogte van de waterkolom van 14 tot 15 m.

Dit lijkt erg op wat er gebeurt met die rietjes die meerdere keren in zichzelf ronddraaien. Door de vloeistof op te zuigen, ontstaat er een drukverschil waardoor de vloeistof naar de mond stijgt.

De maximale hoogte van de kolom bereikt door capillariteit is theoretisch, omdat de straal van de haarvaten niet kan worden verminderd tot voorbij een bepaalde limiet.

Wet van Poiseuille

Dit stelt vast dat de stroom van een echte vloeistof wordt gegeven door de volgende uitdrukking:

Q = (πr⁴/ 8ηl) AP

Waar Q de vloeistofstroom is, is η de viscositeit ervan, l de lengte van de buis en AP het drukverschil.

Bij het verlagen van de straal van een capillair, zou de hoogte van de vloeistofkolom die wordt bereikt door capillariteit voor onbepaalde tijd moeten toenemen. Poiseuille wijst er echter op dat het verminderen van de straal ook de stroom vloeistof door dat capillair vermindert.

Bovendien zou de viscositeit, die een maat is voor de weerstand die de stroming van een echte vloeistof tegenwerkt, de stroming van de vloeistof verder doen afnemen.

-Contacthoek (θ)

Hoe hoger de waarde van de cosθ, hoe hoger de hoogte van de waterkolom door capillariteit, zoals aangegeven door Jurin's Law.

Als θ klein is en de waarde nul (0) nadert, is cosθ = 1, dus de waarde h is maximaal. Integendeel, als θ gelijk is aan 90º, cosθ = 0 en de waarde van h = 0.

Wanneer de waarde van θ groter is dan 90º, wat het geval is voor de convexe meniscus, stijgt de vloeistof niet door capillariteit en is zijn neiging om af te dalen (zoals gebeurt met kwik).

Capillillariteit van water

Het water heeft een oppervlaktespanningswaarde van 72,75 N / m, relatief hoog in vergelijking met de waarden voor oppervlaktespanning van de volgende vloeistoffen:

-Aceton: 22,75 N / m

-Ethylalcohol: 22,75 N / m

-Hexaan: 18,43 N / m

-Methanol: 22,61 N / m.

Daarom heeft water een uitzonderlijke oppervlaktespanning, wat gunstig is voor de ontwikkeling van het capillaire fenomeen dat zo noodzakelijk is voor de opname van water en voedingsstoffen door planten.

Op de planten

De capillariteit is een belangrijk mechanisme voor de opkomst van het sap door het xyleem van de planten, maar het is op zichzelf onvoldoende om het sap de bladeren van de bomen te laten bereiken.

De transpiratie of verdamping is een belangrijk mechanisme bij de opstijging van het sap door het xyleem van de planten. De bladeren verliezen water door verdamping, waardoor een afname van de hoeveelheid watermoleculen wordt veroorzaakt, waardoor de watermoleculen in de capillaire buizen aangetrokken worden (xyleem).

De watermoleculen werken niet onafhankelijk van elkaar, maar werken samen door de Van der Waals-krachten, waardoor ze opstijgen verbonden door de capillaire buizen van de planten naar de bladeren.

Naast deze mechanismen moet worden opgemerkt dat de planten water uit de grond absorberen door middel van osmose en dat een positieve druk die wordt gegenereerd aan de wortel, het begin van de opstijging van water door de haarvaten van de plant stuurt.

referenties

1. García Franco A. (2010). Oppervlakkige verschijnselen. Teruggeplaatst van: sc.ehu.es
2. Oppervlakteverschijnselen: oppervlaktespanning en capillariteit. [PDF]. Opgehaald van: ugr.es
3. Wikipedia. (2018). Capillariteit. Teruggeplaatst van: en.wikipedia.org
4. Risvhan T. (s.f.) Capillariteit in de planten. Teruggeplaatst van: academia.edu
5. Helmenstine, Anne Marie, Ph.D. (22 december 2018). Capillaire actie: definitie en voorbeelden. Teruggeplaatst van: thoughtco.com
6. Ellen Ellis M. (2018). Capillaire werking van water: definitie en voorbeelden. Study. Teruggeplaatst van: study.com
7. ScienceStruck-medewerkers. (16 juli 2017). Voorbeelden die het concept en de betekenis van capillaire actie verklaren. Teruggeplaatst van: sciencestruck.com