Broglie Atomic Model Kenmerken en Beperkingen
de Broglie atomisch model werd voorgesteld door de Franse natuurkundige Louis Broglie in 1924. In zijn proefschrift beweerde Broglie de golfdeeltjes dualiteit van elektronen, de basis leggend voor de golfmechanica. Broglie publiceerde belangrijke theoretische bevindingen over de golf-corpusculaire aard van materie op atomaire schaal.
Vervolgens werden de Broglie-uitspraken experimenteel aangetoond door de wetenschappers Clinton Davisson en Lester Germer in 1927. De Broglie-elektronengolftheorie is gebaseerd op het voorstel van Einstein over de golfeigenschappen van licht bij korte golflengten.
Broglie kondigde de mogelijkheid aan dat materie een gedrag had dat vergelijkbaar was met dat van licht, en suggereerde vergelijkbare eigenschappen in subatomaire deeltjes zoals elektronen.
Elektrische ladingen en banen beperken de amplitude, lengte en frequentie van de golf die door elektronen wordt beschreven. Broglie verklaarde de beweging van elektronen rond de atoomkern.
index
- 1 Kenmerken van het Broglie-atomisch model
- 2 Davisson en Germer experiment
- 3 Beperkingen
- 4 artikelen van belang
- 5 Referenties
Kenmerken van het atomaire model van Broglie
Om zijn voorstel te ontwikkelen, ging Broglie uit van het principe dat elektronen een tweevoudig karakter hadden tussen golf en deeltje, vergelijkbaar met licht.
In deze zin maakte Broglie een vergelijking tussen beide fenomenen, en op basis van de vergelijkingen die Einstein had ontwikkeld voor de studie van de golfkarakteristiek van licht, gaf hij het volgende aan:
- De totale energie van het foton en, bijgevolg, de totale energie van het elektron, resulteert uit het product van de frequentie van de golf en de Plank-constante (6.62606957 (29) × 10 -34 Jules x seconden), zoals beschreven in de volgende uitdrukking:
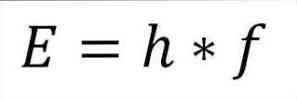
In deze uitdrukking:
E = elektronenenergie.
h = Plankconstante.
f = frequentie van de golf.
- Het lineaire moment van het foton en dus van het elektron is omgekeerd evenredig met de golflengte, en beide magnituden zijn gerelateerd door de Plank-constante:
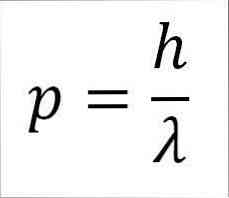
In deze uitdrukking:
p = lineair moment van het elektron.
h = Plankconstante.
λ = golflengte.
- Het lineaire momentum is het product van de massa van het deeltje door de snelheid die het deeltje tijdens zijn verplaatsing heeft.
Als de vorige wiskundige uitdrukking is geherstructureerd als een functie van de golflengte, hebben we het volgende:
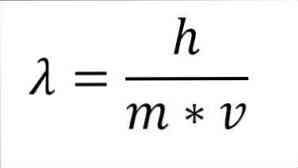
In de genoemde uitdrukking:
λ = golflengte.
h = Plankconstante.
m = massa van het elektron.
v = elektronensnelheid.
Omdat h, de Plank-constante, een kleine waarde heeft, is de golflengte λ ook. Bijgevolg is het mogelijk om te stellen dat de golfeigenschappen van het elektron alleen op atomaire en subatomaire niveaus voorkomen.
- Broglie is ook gebaseerd op de postulaten van het atoommodel van Bohr. Volgens de laatste zijn de banen van de elektronen beperkt en kunnen het alleen veelvouden zijn van gehele getallen. dus:
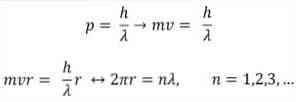
waarbij:
λ = golflengte.
h = Plankconstante.
m = massa van het elektron.
v = elektronensnelheid.
r = straal van de baan.
n = geheel getal.
Volgens het Bohr-atoommodel, dat door Broglie als basis werd aangenomen, zijn de elektronen die zich als staande golven gedragen, de enige toegestane banen die met een straal die gelijk is aan een integraal veelvoud van de golflengte λ..
Daarom voldoen niet alle banen aan de parameters die een elektron nodig heeft om er doorheen te bewegen. Dat is de reden waarom de elektronen alleen in specifieke banen kunnen reizen.
De golftheorie van de Broglie-elektronen rechtvaardigde het succes van het Bohr-atoommodel om het gedrag van het enkele elektron van het waterstofatoom te verklaren.
Op dezelfde manier werpt het ook licht op waarom dit model niet paste bij meer complexe systemen, dat wil zeggen atomen met meer dan één elektron.
Davisson en Germer experimenteren
De experimentele verificatie van het atoommodel Broglie vond plaats 3 jaar na de publicatie ervan, in 1927.
De vooraanstaande Amerikaanse natuurkundigen Clinton J. Davisson en Lester Germer bevestigden experimenteel de theorie van golfmechanica.
Davisson en Germer voerden verstrooiingsproeven uit van een elektronenbundel door een nikkelkristal en observeerden het diffractieverschijnsel door het metaalmedium.
Het uitgevoerde experiment bestond uit het uitvoeren van de volgende procedure:
- In eerste instantie werd een assemblage met een elektronenbundel geplaatst die een bekende initiële energie had.
- Er is een spanningsbron geïnstalleerd om de beweging van elektronen te versnellen, wat een mogelijk verschil tot gevolg heeft.
- De stroom van de elektronenbundel was gericht op een metaalkristal; in dit geval, nikkel.
- Het aantal elektronen dat een impact had op het nikkelkristal werd gemeten.
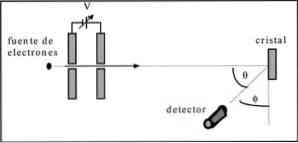
Aan het einde van het experiment ontdekten Davisson en Germer dat de elektronen in verschillende richtingen waren verspreid.
Door het experiment te herhalen met behulp van metaalkristallen met verschillende oriëntaties, ontdekten de wetenschappers het volgende:
- De dispersie van de elektronenbundel door het metaalkristal was vergelijkbaar met het verschijnsel van interferentie en diffractie van de lichtstralen.
- De reflectie van de elektronen op het impactkristal beschreef het traject dat theoretisch zou moeten worden beschreven volgens de theorie van de elektronengolven van Broglie..
In synthese, het experiment van Davisson en Germer experimenteel bewezen de dual wave-deeltjes aard van elektronen.
beperkingen
Het atoommodel van Broglie voorspelt niet de exacte locatie van het elektron in de baan waarin het beweegt.
In dit model worden elektronen waargenomen als golven die zich zonder een specifieke locatie in de baan bewegen, wat het concept van een elektronische orbitaal introduceert.
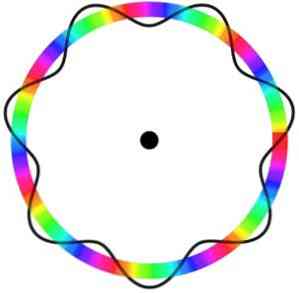
Bovendien houdt het atomaire model van Broglie, analoog aan het model van Schrödinger, de rotatie van elektronen op zijn as niet in (spinnen).
Door het intrinsieke impulsmoment van elektronen te negeren, worden de ruimtelijke variaties van deze subatomaire deeltjes verwaarloosd..
In dezelfde volgorde van ideeën houdt dit model geen rekening met veranderingen in het gedrag van snelle elektronen als gevolg van relativistische effecten.
Artikelen van belang
Atoommodel van Schrödinger.
Atoommodel van Chadwick.
Atoommodel van Heisenberg.
Atoommodel van Perrin.
Atoommodel van Thomson.
Atoommodel van Dalton.
Atoommodel van Dirac Jordan.
Atoommodel van Democritus.
Atoommodel van Bohr.
referenties
- Bohr's Quantum Theory en De Broglie Waves (s.f.). Teruggeplaatst van: ne.phys.kyushu-u.ac.j
- Louis de Broglie - Biographical (1929). © De Nobel Foundation. Teruggeplaatst van: nobelprize.org
- Louis-Victor de Broglie (s.f.). Teruggeplaatst van: chemed.chem.purdue.edu
- Lovett, B. (1998). Louis de Broglie. Encyclopædia Britannica, Inc. Opgehaald van: britannica.com
- Atoommodel van De Broglie. Nationale universiteit voor afstandsonderwijs. Spanje. Teruggeplaatst van: ocw.innova.uned.es
- Waves Of Matter Of Louis De Broglie (s.f.). Teruggeplaatst van: hiru.eus
- Von Pamel, O., en Marchisio, S. (s.f.). Kwantummechanica Nationale universiteit van Rosario. Teruggeplaatst van: fceia.unr.edu.ar


