Heptagonal Prism-functies en hoe het volume te berekenen
een zevenhoekig prisma is een geometrische figuur die, zoals de naam aangeeft, twee geometrische definities omvat die: prisma en heptagon zijn.
Een "prisma" is een geometrische figuur begrensd door twee basen die gelijke en evenwijdige veelhoeken zijn en hun zijvlakken zijn parallellogrammen.
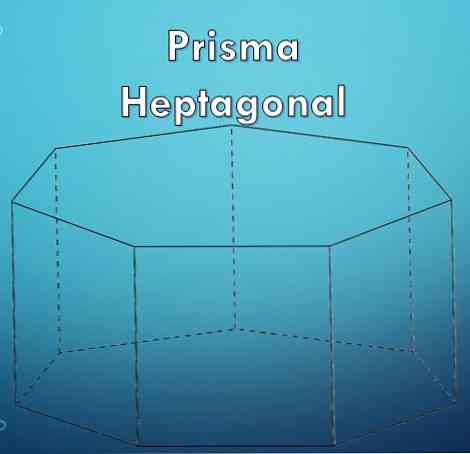
Een "heptagon" is een veelhoek die wordt gevormd door zeven (7) zijden. Omdat een heptagon een polygoon is, kan het zijn dat deze regelmatig of onregelmatig is.
Van een polygoon wordt gezegd dat hij regelmatig is als alle zijden even lang zijn en hun interne hoeken hetzelfde meten, ze worden ook wel gelijkzijdige polygonen genoemd; anders wordt er gezegd dat de polygoon onregelmatig is.

Kenmerken van een zevenhoekig prisma
Hierna volgen bepaalde functies die een zevenhoekig prisma hebben, zoals: de constructie, de eigenschappen van de basis, het oppervlak van alle vlakken en het volume.
1- Constructie
Om een heptagonaal prisma te construeren zijn twee heptagons nodig, die de bases en zeven parallellogrammen zullen zijn, een aan elke zijde van de heptagon.
Begin met het tekenen van een zevenhoek en teken vervolgens zeven verticale lijnen van gelijke lengte, die uit elk van zijn hoekpunten komen.
Tenslotte wordt een andere heptagon getekend zodat de hoekpunten samenvallen met het einde van de lijnen die in de vorige stap zijn getekend.
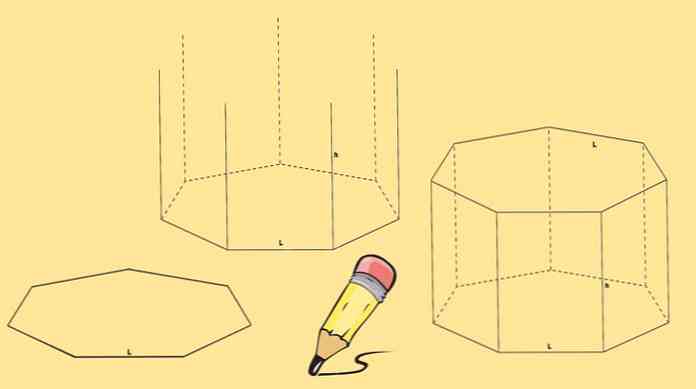
Het heptagonale prisma dat hierboven is getekend, wordt een recht hexagonaal prisma genoemd. Maar je kunt ook een schuin zeshoekig prisma hebben zoals in de volgende afbeelding.

2- Eigenschappen van zijn basissen
Omdat hun basen heptagons zijn, voldoen ze dat het diagonale getal D = nx (n-3) / 2 is, waarbij "n" het aantal zijden van de veelhoek is; in dit geval hebben we dat D = 7 × 4/2 = 14.
We kunnen ook zien dat de som van de interne hoeken van een heptagon (normaal of onregelmatig) gelijk is aan 900º. Dit kan worden geverifieerd door de volgende afbeelding.
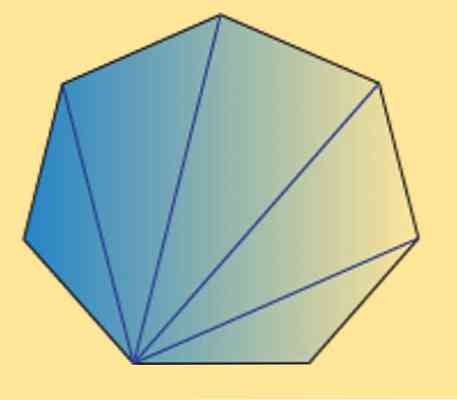
Zoals je kunt zien, zijn er 5 interne driehoeken en het gebruik van de som van de interne hoeken van een driehoek is gelijk aan 180º, het kan worden verkregen dat het gewenste resultaat.
3- Gebied moest een Heptagonal Prism bouwen
Omdat de basen twee heptagons zijn en de zijden zeven parallellogrammen zijn, is het gebied dat nodig is om een heptagonaal prisma te construeren gelijk aan 2xH + 7xP, waarbij "H" het gebied van elke heptagon is en "P" het gebied van elk parallellogram.
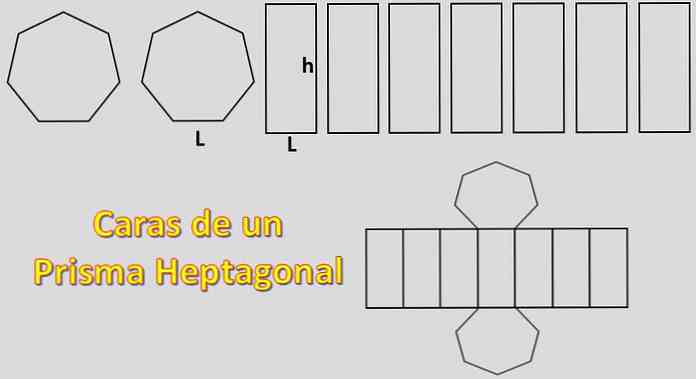
In dit geval wordt het gebied van een normale heptagon berekend. Hiervoor is het belangrijk om de definitie van apothema te kennen.
De apothem is een loodlijn die loopt van het midden van een regelmatige polygoon tot het middelpunt van een van zijn zijden.
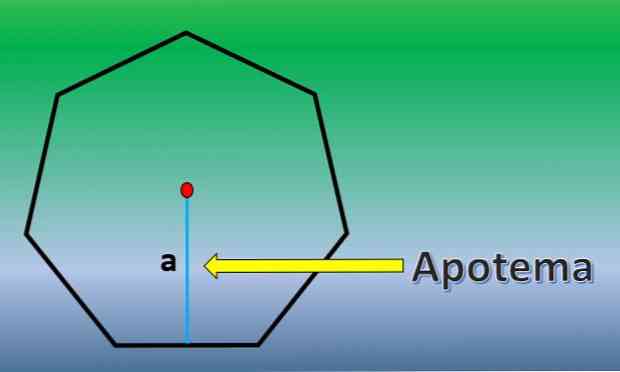
Als het apothem eenmaal bekend is, is het gebied van de heptagon H = 7xLxa / 2, waarbij "L" de lengte is van elke zijde en "a" de lengte van de apotheker..
Het oppervlak van een parallellogram is eenvoudig te berekenen, wordt gedefinieerd als P = Lxh, waarbij "L" dezelfde lengte van de zijkant van de heptagon is en "h" de hoogte van het prisma is.
Concluderend, de hoeveelheid materiaal die nodig is om een heptagonaal prisma te bouwen (met regelmatige basen) is 7xLxa + 7xLxh, dat is 7xL (a + h).
4- Volume
Als het gebied van een basis en de hoogte van het prisma bekend zijn, wordt het volume gedefinieerd als (basisgebied) x (hoogte).
In het geval van een heptagonaal prisma (met regelmatige basis) heeft dit dat het volume V = 7xLxaxh / 2 is; kan ook worden geschreven als V = Pxaxh / 2, waarbij "P" de omtrek van de normale heptagon is.
referenties
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Wiskunde: een probleemoplossende aanpak voor leraren in het basisonderwijs. López Mateos-bewerkers.
- Fregoso, R. S., & Carrera, S. A. (2005). Wiskunde 3. Redactie Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Wiskunde 6. Redactie Progreso.
- Gutiérrez, C. T., & Cisneros, M.P. (2005). 3e Wiskunde Cursus. Redactie Progreso.
- Kinsey, L., & Moore, T.E. (2006). Symmetrie, vorm en ruimte: een inleiding tot de wiskunde door middel van geometrie (geïllustreerd, herdrukt). Springer Science & Business Media.
- Mitchell, C. (1999). Dazzling Math Line Designs (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Ik teken 6º. Redactie Progreso.


